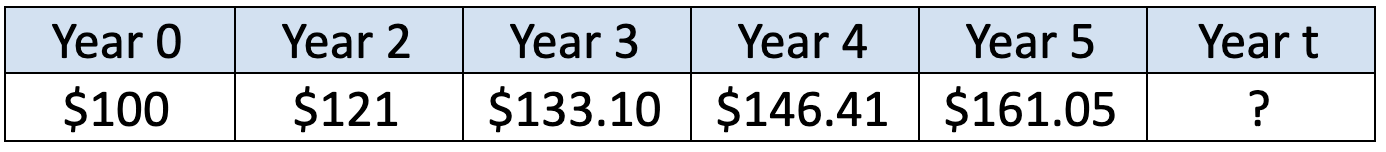As part of my continuing efforts to successfully celebrate my next wedding anniversary, I agreed (cheerfully, I think) to watch Little Women. Period dramas, like this one, always have enough people with enough inherited money that the plot is not bogged down by too many people having to go to work. Nevertheless, there were plenty of bits in the movie to reference how poor the people of the mid-19th century were compared to today. The huge difference in incomes between 1861 (roughly when Little Women took place) and now helps illustrate the absurdity of calling for more and more costly climate policies to account for intergenerational equity.
A recent executive order from President Biden calls for revising the social cost of carbon (SCC) as soon as possible. The SCC purports to estimate the total damage of emitting a ton of carbon dioxide (CO2) between its year of emission and centuries from now. The SCC is to be a guide to determine which policies are worthwhile and the level for any carbon tax.
Though the complexity and difficulty of predicting impacts centuries from now lead to huge uncertainties, in practice, the single most impactful parameter in these calculations is the discount rate used to compare the benefit of climate policies to the benefit of other investments. This discount rate is widely misunderstood to be a way of diminishing the importance of benefits and costs to those who live generations from now. With that misunderstanding in place, climate planners argue that lower discount rates create greater intergenerational equity because they justify greater expense now for any future climate benefit.
Infantilizing the future allows this bizarre twist that regards greater transfers from a poorer generation to a richer one as more equitable. Appeals to sacrificing more for future generations has an undercurrent that regards our grandchildren as no more capable at age fifty than they are at age five. They need us and without our conscious assistance (now and always), they are helpless in the face of adversity of all sorts.
Since it may be hard to imagine our descendants having capacities and resources orders of magnitude greater than our own, it might be easier to illustrate the perverse appeal to intergenerational equity by comparing ourselves to our impoverished ancestors instead of our wealthy descendants.
We do not have to rely on Hollywood adaptations of semi-biographical novels to learn about these income disparities; we can look at data. These data show that the real (adjusted for inflation to 2012 dollars) per capita GDP in the US for 1861 (when Little Women took place) was $2,943. The same data show the per capita GDP in 2019 was $58,056—a twenty-fold increase in income. This rate of income growth is well within the ballpark of future estimates for world GDP growth. Even these large improvements do not fully capture the benefits of improved technology, like antibiotics that (spoiler alert) could have cured Meg of scarlet fever.
Whatever Meg, Jo, Amy, Beth and everybody else in 1861 could have done to cut a ton of CO2 emissions can be considered a climate investment. Whatever mitigation in climate damage that old cut in CO2 give us today is the payoff from that investment. The SCC is an attempt to guide us in undertaking the climate investments that make sense while skipping the ones that do not. Part of that exercise is a process called discounting.
Discounting need not be a mystery. It is simply the inverse of compound interest. A brief review may help. For simplicity in illustrating the concept, we will use round numbers and assume there is a savings account that pays ten percent interest. With a deposit of $100 the balance in the account would grow to $110 after one year. Again, for simplicity, let us assume that there are no taxes on the interest and no withdrawals. Each subsequent year the balance will be ten percent larger than the year before.
Year 0 is when the deposit is made. The value in one year is 1.1 times the value in the previous year, where the “.1” is the decimal version of ten percent. This can also be written (1+.10). That term, (1+.10), is added to calculation for the previous year in a daisy-chain fashion. It would look like this: $100(1+.10)(1+.10)(1+.10)… for as many years into the future as needed. All those terms can be collected in exponential form so we get $100(1+.10)ᵗ. For example, if we leave that money in the bank for 50 years the value at the end will be $100(1.1)⁵⁰=$11,739.09.
Discounting, which calculates the present value works in reverse starting with that last year. In this example, $100 is the present value of the $11,739.09 future value.
We would say that $100 is the present value of $11,739.09 received in 50 years, discounted at ten percent. At the risk of causing a rash to those with an allergy to algebra, we can write the generic equation for compounding like this:
FV=PV(1+r)ᵗ
Here, FV is future value, PV is present value, r is the interest rate and t is the number of years.
Simple division gives the formula for calculating the present value:
PV=FV/(1+r)ᵗ
In this case r is called the discount rate.
Discounting is used to determine whether an investment pays at least as well as a reasonably available alternative investment. For instance, sticking with the case above, if somebody said they would sell you a tree farm whose value upon harvesting in 50 years would be $10,000, the highest price you should pay would be (using the PV formula above) $85.19. For any price above that, it makes more sense to put the money in the bank account and get a larger payout from the compounding at ten percent.
That is all discounting does. It does not compare the relative worth of people in different periods or what inflation does or how incomes grow. It simply says how much you would have to invest, elsewhere, today, to get that future value later.
Of course, using the wrong discount rate will give incorrect present values. If discounting is used to guide policy (such as in the SCC determination) the wrong interest rate will misguide the policy.
Between 1802 and 2002, the before-tax (which is the relevant measure, here) real rate of return on the New York Stock Exchange averaged between 7.5 percent per year and 9.9 percent per year. A seven percent discount rate is consistent with Office of Management and Budget guidance and is sufficiently close to the real return on the NYSE, to illustrate the problem with the lower rates. Nevertheless, some argue for using a discount rate as low as one percent.
One argument for using a lower discount rate is for greater intergenerational equity. That argument is exactly backwards.
Calculating the relative impacts of discounting at one percent vs. higher rates (such as seven percent) illustrates which rates lead to greater equity. Suppose certain CO2 emission in 1861 would cause climate damage in 2019 valued at $2,000. Further suppose, this 2019 damage could have been avoided by cutting a ton of CO2 emissions in 1861. Discounting $2,000 over that time span at one percent gives a present value (in 1861) of $415.
According to the logic driving the SCC calculations, it would have been appropriate to force people in 1861 to reduce CO2 emissions by a ton (Jo sure seemed to use a lot of candles when she wrote at night) so long as the cost were no more than $415. The $415 loss in 1861 for a gain of $2,000 in 2019 trades off 14 percent of a person’s income in 1861 to provide a three-percent-of-income benefit in 2019. It is far from obvious that this tradeoff is equitable. In any event, it is a horrible investment regardless of whether you are looking at it from 1861 or 2019.
Whether or not it is fair to force those 158 years ago to sacrifice a larger share of their income in order to provide a benefit that is a smaller share of a richer generation’s income, we can ask a different, but relevant question: How much could that same $415 climate investment have generated if the investment were made in New York Stock Exchange companies instead? Using the future value formula, above, we see that the $415 could have created additional capital worth an astounding $18,225,731 in 2019. Remember, that seven percent return is already adjusted for inflation.
Perhaps a case can be made for policies that further enrich an already wealthier group at the expense of a poorer group if the gain to the rich is more than the loss to the poor, but it will not be made, here. Fair or not, it is a bad deal when the opportunity cost of the $415 climate investment is considered.
There may be a case for inefficient transfers from the rich to the poor, but not for making inefficient transfers from the poor to the rich. Setting policies levels using a too-low discount rate can make these inefficient, reverse-Robin Hood transfers a reality.
The whole point of discounting is an exercise in opportunity cost. That is, what else could we have reasonably expected to get in the future for our investment of resources today? It is not an exercise in weighing the relative importance of people in different generations. For this opportunity cost exercise to work, the interest rate for discounting should be the best rate that could reasonably be expected. Seven percent is a much better fit than anything below it as it reflects the average return to all the companies on the New York Stock Exchange over that period and is similar to the real return on the Standard & Poors 500 between 1928 (immediately before the Great Depression) and 2014.
The seven percent discount rate may look unfair when alternative investments are not considered. Using seven percent to discount the $2,000 climate benefit in 2019 gives a present value in 1861 of less than a nickel. At first blush, it may seem wholly unreasonable not to spend more than a nickel to give the future generation $2,000. As amazing as it may seem, that nickel invested at seven percent would grow to $2,000 in 2019.
Because of the alternatives available, spending more than a nickel on that CO2 policy 1861 would deny those in 2019 a superior alternative benefit exceeding the $2,000 climate benefit. Neither generation is better off by making a worse investment in 1861.
The discussion about the discount rate and the SCC are more than just the wonk equivalent of guessing at the number of angels that could dance on the head of a pin. The SCC will be used to justify costly regulation and the more the wonks can juice its value, the more you will pay for gasoline, heating, hot water, and everything else (because the price of everything else will have to cover higher energy costs, too).
There is growing pressure in DC to enact a carbon tax and the level of that tax will parallel whatever SCC they can gin up. SCC estimates using the Nobel Prize winner, William Nordhaus’s, economic model show that while a 7-percent discount rate would justify a SCC of $6.70 a 2.5-percent rate would produce an SCC of $61.48, a nine-fold increase. Using an even lower discount rate, some have argued that the SCC should be $200 now and rise every year afterward.
If, as some want, the government used that SCC to impose a $200/ton carbon tax, it would add a $1.80 to the cost of each gallon of gasoline. A carbon tax at that level would take another $2,000 per household just for its impact on gasoline prices. This is on top of the other state, local, and federal gasoline taxes. The increased cost of electricity, home heating and the embedded energy costs of other consumer items would only add to that tax bill.
The world of Little Women was a harsher, poorer, and technologically cruder world than the one we live in today. In similar fashion, the next 160 years (which will take us barely half-way through Biden Administration’s SCC time horizon) will likely bring increases in wealth and technology that are beyond our imagination. Using an inefficiently low discount to game the SCC estimates can in no way be considered a tool for greater intergenerational equity. Such jiggering of the already sketchy SCC calculations would further tax the poorer current world so that future residents would get a speculative bump to their much greater income.