Energy makes modern society possible. It lights the night, heats our homes, powers our entertainment, and most importantly, it helps us conserve the ultimate non-renewable resource—time. Energy amplifies our ability to do work. Machines help autoworkers assemble cars, power tools help construction workers build our homes, gasoline-powered automobiles help us take care of our families, diesel-power trucks distribute fresh produce across the country, and electricity-powered computers give us unprecedented access to information. But the energy that supplies 85 percent of our needs—coal, oil, and natural gas—are under attack. Politicians and special interest groups are proposing various methods to tax these abundant and reliable sources of energy.
The newest attack on oil, natural gas, and coal are proposals to tax carbon dioxide emissions. Noted economist Art Laffer and current U.S. Rep. Bob Inglis (R-S.C.) argued in favor of a carbon tax in a New York Times[1] op-ed. Author, commentator, and syndicated columnist Charles Krauthammer made his case for a large increase in the gas tax in the Weekly Standard .[2] And Fred Smith, the CEO of FedEx, has publicly declared his support for a tax on carbon dioxide emissions.
The arguments boil down to the assertion that carbon taxes are favorable because they are better than cap and trade schemes. This is correct, but it does not mean that we should implement carbon taxes. Carbon tax implementation would run into many of the same problems that have plagued cap and trade. Politicians cannot resist new opportunities to raise tax revenues and dole out our dollars to favored constituencies, especially when the revenues range from hundreds of billions to trillions of dollars. Carbon taxes might hold some allure, but ultimately they are economically destructive. Neither carbon tax nor cap and trade is good for American consumers.
Reasons Why Carbon and Energy Taxes are a Bad Idea:
1. Carbon taxes are taxes on 85 percent of the energy we use. A carbon tax would impose a new tax on the vast majority of our nation’s economic activity. Fossil fuels power our nation and produce 85 percent of the energy we consume in the United States. [3] Nuclear and hydro power produced an additional 11 percent of our energy.[4] The remaining 4 percent comes from other renewables like biofuels, wind, and solar.[5] Carbon taxes may make hydro and nuclear power more attractive, but few sites remain where it is possible to build large hydroelectric dams and new nuclear power plants face major political obstacles.
2. A carbon tax that is perfectly offset by other tax cuts is neither a practical nor a political reality. The history and nature of politics shows that once politicians institute a tax, they will not give it up. Still, some argue in favor of a “tax swap” to reduce income taxes while implementing a new tax on carbon dioxide emissions. Theoretically, this could make sense. However, the argument does not reflect political reality.
The first challenge for promoters of a carbon tax “tax swap” is getting lawmakers to pass a carbon tax. Lawmakers are very wary of imposing easily identifiable taxes across the entire population. Instead, politicians prefer to hide the costs of government programs, while rewarding discrete and identifiable groups. Implementing carbon taxes would result in an identifiable tax increase similar to the unpopular gas tax increases that led to voter displeasure revolts against President George H.W. Bush and President Bill Clinton.
The second challenge for promoters of a “tax swap” is getting Congress to reduce income taxes. Congress could decrease some income taxes, but it is highly unlikely income taxes would be decreased for all income brackets.
Taxpayers will likely fight against a “tax swap” because they understand there is nothing to stop future lawmakers from increasing carbon taxes or returning income taxes to their former levels. Worse, from a taxpayer’s perspective, a carbon tax will give lawmakers another vehicle to raise large amounts of tax revenue.
Some argue that a revenue-neutral “tax swap” would be economically beneficial. There is, however, little evidence politicians are concerned about the economic effectiveness of plans to reduce carbon dioxide emissions. Most economists agree that carbon taxes are a superior to cap and trade.[6] Carbon taxes are more transparent, more understandable, and less subject to political manipulation. Though economists prefer carbon taxes, congressmen strongly prefer cap and trade plans.[7] Lawmakers have floated many cap and trade proposals, but they have not discussed any serious carbon tax proposals.
Lawmakers say they favor economically efficient global warming plans, but their actions demonstrate that the discussion about efforts to reduce greenhouse gas emissions is not about science or economics—it is about politics. Offsetting income taxes with carbon taxes is not a political reality because politicians will not propose such obvious tax increases on all Americans.
3. Politicians like to reward special interest groups with new tax revenues. When politicians have large amounts of tax dollars at their disposal, they tend to spend it on projects that reward special interest groups. A carbon tax would likely generate over $1 trillion in new revenue. Much of this revenue would likely be spent on inefficient “pork” projects.
The proposed cap and trade schemes contain hundreds of billions of dollars for special interests. The recession has spurred additional calls for hundreds of billions of dollars in additional spending to create “green jobs.” For example, the Center for American Progress is calling on Congress to spend $100 billion to create two million “green jobs”[8] and the Apollo Alliance wants Congress to spend $500 billion to create five million “green jobs.”[9] If a carbon tax were in place, lawmakers would almost certainly divert resources to “green job” subsidies or other similar programs, rather than back into taxpayers’ wallets.
4. It is impossible to create an optimal carbon tax. A carbon tax would need to be set at an optimal level that accounts for the economy and climate science. This is an impossible task. One of the greatest insights of the 20th century was that economically efficient central planning is not possible. Friedrich Hayek and others demonstrated that central planners cannot aggregate all of the information necessary to make economically efficient choices.[10] Their insight remains true today. A planner (or Congress) cannot create an optimal tax because he or she does not have all of the necessary information. With global warming, the lack of perfect information is further compounded by partisan politics and uncertain climate science. This makes it impossible to determine an optimal carbon tax.
The cost of a carbon tax will increase the costs of nearly everything that is produced, manufactured, or transported, including food and gasoline. How one would construct a credible methodology for accurately and precisely measuring and accounting for these effects remains, perhaps intentionally, an unaddressed question.
5. A carbon tax is a regressive tax, but increased wealth transfers will likely make it increasingly progressive. Lower income families spend more of their income on energy than higher income families. The Wall Street Journal explains:
The Congressional Budget Office—Mr. Orszag’s former roost—estimates that the price hikes from a 15% cut in emissions would cost the average household in the bottom-income quintile about 3.3% of its after-tax income every year. That’s about $680, not including the costs of reduced employment and output. The three middle quintiles would see their paychecks cut between $880 and $1,500, or 2.9% to 2.7% of income. The rich would pay 1.7%. Cap and trade is the ideal policy for every Beltway analyst who thinks the tax code is too progressive (all five of them).[11]
It appears that some of the proponents of carbon taxes are some of those five beltway analysts who believe the tax code is too progressive. They argue in favor of a carbon tax because it will not retard the formation of capital because it applies to everyone. In other words, since it would be spread over the population without regard to income, carbon tax proponents argue it will not reduce the incentives for high-income earners to generate wealth and create new jobs.
This alleged advantage, however, would never last politically because a carbon tax will be a visible and ever-increasing new tax. In response to that reality, lawmakers are likely to execute new, politically popular transfers of wealth—all with an eye on limiting the tax’s effect on lower-income families. Sales taxes, for example, could be uniformly applied across the economy, but in practice, sales taxes vary on certain items, in part, to help lower-income Americans deal with the increased costs imposed by them.
Carbon taxes would likely be accompanied by various rebate schemes to soften the regressive nature of the tax and make it a more progressive tax. This is currently happening with cap and trade proposals. One plan calls for the government to auction all emission permits and give each citizen a $700 check every year.[12] Another option is to only give the rebate checks from auction revenues to lower-income citizens.[13]
If the government imposes a carbon tax, it is very unlikely that the tax will remain uniform. In the end, not only will it hit the poor with a disproportionate burden of a carbon cap, but it will create yet another series of loopholes in the tax code. As history has shown, such a plan will further distort the market, render the tax code even more complicated, and hide yet another round of handouts to well-connected special interests.
6. A carbon tax set at a wrong level will cause great economic harm. Even the proponents of carbon taxes, such as Yale University Professor William Nordaus, find that once there is deviation from worldwide participation, the costs of achieving environmental global improvements dramatically rise. Nordhaus’ economic model shows that an overly ambitious and/or inefficiently structured policy can swamp the potential benefits of a perfectly calibrated and efficiently targeted plan.[14] For example, Nordhaus’ optimal plan yields net benefits of $3 trillion ($5 trillion in reduced climatic damages and $2 trillion in abatement costs). Yet, other popular proposals have abatement costs that exceed their benefits. The worst is former Vice President Al Gore’s 2007 proposal to reduce carbon dioxide emissions 90 percent by 2050. Nordhaus’ model estimates this plan would make the world more than $21 trillion poorer than if there were no controls on carbon dioxide.[15]
7. Realistically, a carbon tax would lead to lower energy use and lower economic output because low-carbon replacement technologies simply do not exist. Carbon taxes effectively increase the cost of fossil fuels in an effort to make non-fossil fuels more economically attractive. The technologies to significantly reduce greenhouse gas emissions from fossil fuels, however, are decades away and extremely costly.[16] Instead, the only real way to reduce greenhouse gas emissions in the short run is to reduce energy use and economic output.
Consider automobile use and gas prices. People have begun to transition toward fuel-efficient cars, but the real impact of high gasoline prices in 2008 was to reduce vehicle miles traveled. Just as higher fuel prices led to less driving, higher energy prices will lead to reduced energy consumption. That will lead to a corresponding drop in our ability to make economic choices.
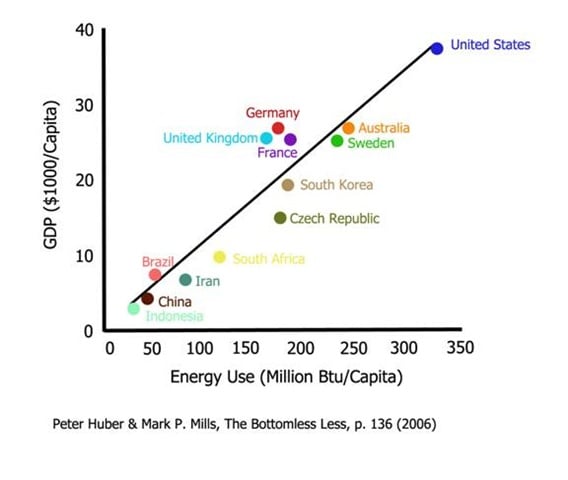
Given current technologies, carbon taxes will result in less economic output. The graphic below illustrates that point. The implication is clear—there is a strong correlation between energy use and GDP.
8. Just because a proposal is “budget neutral” for the government does not mean it is “budget neutral” for American families. Carbon taxes or cap and trade programs will transfer wealth from rural areas, where people drive more and use more energy, to more densely populated urban areas.[17] Not coincidentally, many urban and Northeastern politicians favor a cap and trade program or carbon taxes.
Also, carbon taxes will disproportionally harm states that generate the majority of their electricity from coal-fired power plants.[18] These states tend to be more rural states.
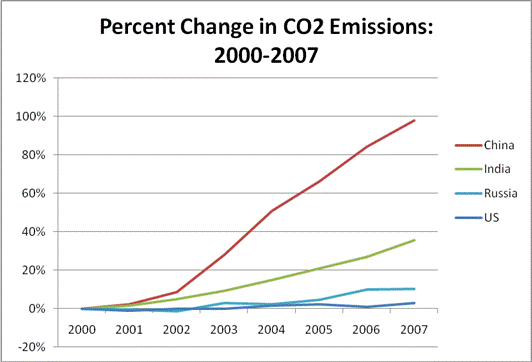
9. Domestic carbon taxes, even in the best case, can only produce marginal impacts on climate. In 2006, China surpassed the United States as the world’s largest emitter of carbon dioxide.[19] But the difference in emission growth rates is striking. According to data from the Global Carbon Project, from 2000 through 2007, global total greenhouse gas emissions increased 26 percent. During that same period, China’s carbon dioxide emissions increased 98 percent, India’s increased 36 percent and Russia’s increased 10 percent. Carbon dioxide emissions in the United States increased by three percent from 2000 through 2007.[20] These data are displayed in the graphic below:
As time goes on, the United States will emit a smaller and smaller share of the world’s total greenhouse gas emissions,[21] which makes unilateral efforts— such as a domestic carbon tax—an ineffective way to influence climate. If the United States were to completely cease using fossil fuels, the increase from the rest of the world would replace U.S. emissions in less than eight years.[22] If we reduced the carbon dioxide emissions from the transportation sector to zero, the rest of the world would replace those emissions in less than two years.[23] Increases in worldwide carbon dioxide emissions are driven by developing economies, not the United States.
10. Domestic carbon taxes will force more industries to leave America. Energy costs are a major expenditure for heavy industry. America’s natural gas prices are the highest in the world,[24] even though we have the world’s sixth largest proven natural gas reserves.[25] The high price of natural gas has significantly contributed to the loss of more than three million manufacturing jobs since 2000.[26] Carbon taxes will drive up the cost of natural gas because companies would use it as a substitute for coal in electricity production, which means increased electricity costs for industry and increased natural gas prices. This is especially troublesome for chemical companies, all of which use natural gas not only as an energy source, but also as a feedstock. Higher natural gas prices will force them to pursue options offshore and overseas, reducing American jobs.
11. Domestic carbon taxes cannot address “leakage.” High costs of doing business in America will force jobs and economic activity to leave this country in favor of countries with lower energy prices. China and India have stated they will not impose burdensome climate regulations on their citizens.[27] Because not all countries will implement carbon taxes, industries will take their jobs to countries where taxes do not eat their profits. Despite a huge American economic sacrifice, global emissions will remain the same.
12. Carbon taxes will lead to calls for trade protectionism. Carbon taxes will lead to reduced economic competitiveness. In turn, organized labor will likely call for new barriers to trade. For example, a top priority for the United Steelworkers is a “border adjustment” to penalize the steel imports from countries that do not curb their greenhouse gas emissions.[28] Increased U.S. trade protectionism will almost certainly lead to greater trade protectionism worldwide that will further harm the American economy and all of America’s trading partners.
13. If we are truly concerned about reducing carbon dioxide emissions, the best path forward is increasing humankind’s ability to adapt. Rich countries and societies can adapt more easily to changed circumstances than poor countries. Environmental improvements are more likely to be realized in prosperous societies than in poorer ones.[29] Carbon taxes and cap and trade reduce society’s aggregate wealth, which make environmental improvements more difficult to achieve.
14. Real world experience counsels against a carbon tax. Ken Green, a former supporter of a revenue-neutral carbon tax, changed his mind because of political and economic realities. Mr. Green writes: [30]
I previously felt that a revenue-neutral carbon tax was a good idea, because it would be both effective and could even be economically beneficial. But three developments have caused me to retract my support. First, rising energy costs have already imposed a huge carbon tax with little GHG reduction. This suggests that the elasticity of energy use could be lower than prior estimates, meaning it would be a useless gesture. Second, as implementations of carbon taxes in Europe and Canada have demonstrated, governments simply cannot implement such tax systems without sucking up some of the revenue, and using the rest to benefit crony-capitalists and steer money to favored constituencies. And finally, because using biofuels such as ethanol would let people save on carbon taxes, demand for such fuels will grow, only compounding the environmental and nutritional mischief they cause.
Just because a carbon tax is a bad idea does not mean that cap and trade is better
Nearly all of the above arguments against a carbon tax apply equally to cap and trade schemes. The only real difference is that cap and trade is a stealth tax that brings a large amount of reporting, implementation, and regulatory problems.
The point of cap and trade plans, like carbon taxes, is to increase the price of energy from oil, coal, and natural gas. Lawmakers may say they have plans to rebate some people so that everyone does not suffer, but it is not possible to craft a cap and trade plan that is perfectly offset by rebates. Just because a politician promotes a plan that is “budget neutral” for government does not mean it is “budget neutral” for American families. When politicians redistribute money, there will be winners and losers. The winners will be the politically well-connected groups and the populace as a whole will lose.
Like carbon taxes, it is not possible to set a cap for cap and trade plans at an optimal level. The smartest people in the world could not aggregate enough data quickly enough to discover the optimal level of the cap or a cap and trade scheme or the level of a carbon tax. It would require too much data about American’s preferences and about uncertain climate science. To complicate matters, if the cap set at the wrong level, or if the plan does not include all nations, the inefficiencies will swamp any possible benefits. Most disturbingly, if the United States unilaterally reduces our carbon dioxide emissions, it will not have a real effect on global carbon dioxide concentrations. This means there will be no environmental benefits to the United States unilaterally reducing carbon dioxide emissions.
Cap and trade schemes are very regressive taxes. They will transfer wealth from poorer areas of the country to wealthier areas. Cap and trade will also reduce energy use and thereby reduce economic output. Also, if we drive up costs, cap and trade plans will reduce American economic competitiveness and cause more jobs to flee to foreign countries.
In short, cap and trade and carbon taxes are two different ways to raise energy prices. Both carbon taxes and cap and trade would harm the United States’ economy without making any meaningful differences in global concentrations of carbon dioxide.
Conclusion
Energy is the lifeblood of the economy. Policies that increase the price of energy harm the economy. However, the entire point of policies like carbon taxes and cap and trade is to increase energy prices. These cost increases make the economy less efficient domestically and it makes the United States less economically competitive internationally. Higher energy prices harms America’s ability to grow its economy at home and it means more American jobs will be shipped overseas.
Now is not the time to implement an economically harmful plan like carbon taxes or cap and trade. Americans need an efficient economy to reverse the recession and improve the lives of American workers. Carbon taxes and cap and trade will just make it more difficult to reverse the recession.
[1] Rep. Bob Inglis & Arthur B. Laffer, An Emissions Plan Conservatives Could Warm To, Dec. 27, 2008, http://www.nytimes.com/2008/12/28/opinion/28inglis.html.
[2] Charles Krauthammer, The Net-Zero Gas Tax: A Once in a Generation Chance, Jan. 5, 2009, http://weeklystandard.com/Content/Public/Articles/000/000/015/949rsrgi.asp
[3] Energy Information Administration, U.S. Energy Consumption by Energy Source, http://www.eia.doe.gov/cneaf/alternate/page/renew_energy_consump/table1.html. (May 2008).
[4] Id.
[5] Id.
[6] See e.g. William D. Nordhaus, Life After Kyoto: Alternative Approaches to Global Warming Policies, NBER Working Paper No. 11889, Dec. 9, 2005, http://www.econ.yale.edu/~nordhaus/homepage/kyoto_long_2005.pdf; N. Gregory Mankiw, One Answer to Global Warming: A New Tax, N.Y. Times, Sept. 16, 2007, http://www.nytimes.com/2007/09/16/business/16view.html; Kenneth P. Green et. al., Climate Change: Cap vs. Taxes, American Enterprise Institute Environmental Policy Outlook, June 1, 2007, http://www.aei.org/publications/filter.all,pubID.26286/pub_detail.asp.
[7] The following is some of the cap and trade bills introduced during the 110th Congress: S. 2191, The Climate Security Act of 2008; S. 1766, the Low Carbon Economy Act, S. 280, the Climate Stewardship and Innovation Act; S. 309, the Global Warming Pollution Reduction Act; S. 485, the Global Warming Reduction Act; H.R. 620, the Climate Stewardship Act; and H.R. 1590, the Safe Climate Act of 2007.
[8] Robert Pollin, et. al, Green Recovery: A Program to Create Good Jobs and Start Building a Low-Carbon Economy, Sept. 2008, http://www.americanprogress.org/issues/2008/09/pdf/green_recovery.pdf.
[9] Jeffery Ball, Does Green Energy Add 5 Million Jobs? Potent Pitch, but Numbers are Squishy, Wall Street Journal, Nov. 7, 2008, http://online.wsj.com/article/SB122601449992806743.html.
[10] See e.g. Friedrich A. Hayek, The Use of Knowledge in Society, 4 Am. Econ. Rev. 519 (Sept. 1945).
[11] Editorial, Who Pays for Cap and Trade? Wall Street Journal, March 9, 2009.
[12] James K. Boyce & Matthew Riddle, Cap and Dividend: How to Curb Global Warming While Protecting the Incomes of American Families, Political Economy Research Institute (Nov. 2007), http://www.peri.umass.edu/fileadmin/pdf/working_papers/ working_papers_101-150/WP150.pdf.
[13] Robert Greenstein et. al., Designing Climate-Change Legislation that Shields Low-Income Households from Increased Poverty and Hardship, Center on Budget and Policy Priorities (May 9, 2008), http://www.cbpp.org/10-25-07climate.pdf.
[14] Robert P. Murphy, Rolling the DICE: Nordhaus’ Dubious Case for a Carbon Tax, p. 20, June 2008, https://www.instituteforenergyresearch.org/wp-content/uploads/2008/06/2008-06_rolling_the_dice_murphy.pdf.
[15] Id. at 20.
[16] See Kenneth P. Green, Climate Change: Science and Policy, Oct. 27, 2008, http://www.aei.org/publications/filter.all,pubID.28838/pub_detail.asp.
[17] Alaska has the higher per capita energy use, followed by Wyoming, Louisiana, North Dakota and Texas. The states with the lowest energy use per capita are Rhode Island, New York, Massachusetts, California, and New Hampshire. The average Rhode Islander uses only 18% as much energy as an Alaskan and 22% as much energy as someone from Wyoming. See Energy Information Administration, Table R2. Energy Consumption by Source and Total Consumption per Capita, Ranked by State, 2006, Nov. 28, 2008, http://www.eia.doe.gov/emeu/states/hf.jsp?incfile=sep_sum/plain_html/rank_use_per_cap.html.
[18] The states with the most affordable electricity either generate the majority of their electricity from coal-fired power plants or from hydro power. See Energy Information Administration, Table S1. Energy Consumption Estimates by Source and End-Use Sector, 2006, State Energy Consumption Estimates: 1960 through 2006, Nov. 2008, http://www.eia.doe.gov/emeu/states/sep_use/notes/use_print2006.pdf; Energy Information Administration, Table 5.6.B. Average Retail Price of Electricity to Ultimate Customers by End-Use Sector, by State, Year-to-Date through September 2008 and 2007, Dec. 12, 2008, http://www.eia.doe.gov/cneaf/electricity/epm/table5_6_b.html.
[19] See e.g. Netherlands Environmental Assessment Agency, China now no. 1 in CO2 emissions; USA in second position, June 19, 2007, http://www.pbl.nl/en/news/pressreleases/2007/20070619Chinanowno1inCO2emissionsUSAinsecondposition.html.
[20] Calculated using the emission data from the Global Carbon Project. In 2000, China emitted 910,950 GgC, India 316,804 GgC, Russia 391,652 GgC, and the U.S. 1,541,013 GgC. By 2007, China emitted 1,801,932 GgC, India 429,601 GgC, Russia 432,486 GgC, and the U.S. 1,586,213 GgC.
[21] According to the Global Carbon project, in 2007, China emitted 21% of the world’s carbon equivalent and the U.S. emitted 19%.
[22] Calculated using the emission data from the Global Carbon Project. According to these data, the U.S. emitted 1,586,213 GgC in 2007. Without the U.S., the world’s emissions were 5,203,987 GgC in 2000, increasing to 6,884,787 GgC in 2007.
[23] Calculated using the emission data from the Global Carbon Project. According to EPA, the GHG emissions from the transportation sector total 28% of total U.S. emissions. Environmental Protection Agency, Regulating Greenhouse Gas Emissions Under the Clean Air Act; Proposed Rule, 73 Fed. Reg. 44354, 44403 (July, 30, 2008). Twenty eight percent of the U.S.’s 2006 carbon dioxide emissions are 436,141 GgC. From 2005 to 2007, the world’s emissions, with the emissions from the U.S., grew by 476,324 GgC.
[24] Paul N. Cicio, Testimony of Paul N. Cicio, President of Industrial Energy Consumers of America before the House of Representatives, Dec. 6, 2007, http://www.ieca-us.com/documents/IECAHouseTestimony-NaturalGas_12.06.07.pdf.
[25] Energy Information Administration, Annual Energy Review 2007, Table 11.4, http://www.eia.doe.gov/emeu/aer/txt/ptb1104.html.
[26] See Testimony of Paul N. Cicio.
[27] See e.g. Shai Oster, China Asks Rich to Pay for Cleanup, Wall Street Journal, Oct. 30, 2008, http://online.wsj.com/article/SB122530768753281185.html; Nitin Sethi, As Climate Talks Resume, India Accuses UN of Bias, The Times of India, Aug. 21, 2008, http://timesofindia.indiatimes.com/Climate_talks_resume_today_India_accuses_UN_of_bias/articleshow/3386789.cms.
[28] Christa Marshall, Report says climate rules could shut down energy-intensive companies, ClimateWire, Feb. 2, 2009.
[29] Bruce Yandle, Environmental Kuznets Curves: A Review of the Findings, Methods, and Policy Implications, 2004, http://www.perc.org/articles/article207.php.
[30] Kenneth P. Green, Climate Change: Science and Policy, http://www.aei.org/publications/filter.all,pubID.28838/pub_detail.asp.