Despite China’s ratification of the Paris global climate agreement, it is still building more coal-fired power plants. So too is Japan, who is replacing its retired nuclear power primarily with natural gas and coal. China, the world’s biggest investor in fossil-fuel generation, began construction on over 70 gigawatts of new coal projects last year while it still had 200 gigawatts under construction. China is spending 1 trillion yuan ($150 billion) by 2020 on what some consider excess power capacity.[i] This puts in question whether China is serious about reducing its greenhouse gas emissions.
Japan has turned toward natural gas and coal, rather than renewables, to replace its nuclear generation. Japanese utilities are resisting renewables because concerns about the costs of renewable energy when fossil-fuel imports are cheap, as well as renewable projects’ safety and environmental impact. Inexpensive coal and natural gas, which is mostly imported, comprise over 75 percent of Japan’s energy needs in the year ended in March, compared with 54 percent in 2010–before the nuclear accident at Fukushima. Japan plans to increase the number of coal-burning power plants by almost 50 percent in the next 12 years.[ii] (See graph below.)

Source: http://www.wsj.com/articles/japans-shift-to-renewable-energy-loses-power-1473818581
Japan
Japan has a goal for renewable energy to provide 22 to 24 percent of its energy needs by 2030. But since 2010, it has increased its renewable share by just 4 percentage points—from 10 percent to 14 percent with most of it hydroelectric power. Instead, it has turned to inexpensive natural gas (LNG, the price of which has dropped considerably) and coal imports for its replacement generation for nuclear power, which went from supplying 29 percent of generation in 2010 to just 1 percent of generation in 2015.
Investment in wind and geothermal power is being hurt by regulatory hurdles and “not in my backyard” opposition, and solar power is facing a pullback in government-mandated prices for the purchase of solar power by utilities. Hydroelectric power has already been built up and few potential and non-controversial sites are left for large-scale plants. Biomass plants are burdened by low efficiency in transforming fuel into power. Sea wave and tidal power are very expensive and there are concerns about potential environmental damage.
As an example of some of the opposition to renewable energy, the building of a geothermal plant in the district where the Fukushima Daiichi meltdown occurred in 2011 ran into serious opposition. Residents were scared by the geothermal power and wanted to be assured that it was safe before exploratory drilling was undertaken.
Developers plan to dig the first exploratory well this fall for a geothermal plant near Mount Bandai in Fukushima, about 130 miles north of Tokyo. It will take about 10 years for a plant to start operating on the site. If this bodes well, geothermal may flourish in Japan since it has the world’s third-largest geothermal reserves, of which only 2.2 percent is harnessed. The government has a target of tripling Japan’s geothermal generating capacity by 2030. So far, it has been held back due to limited access to national parks, where many of the promising locations for large-scale drilling are located, high initial costs, and concerns about naturally occurring heavy metals (e.g. arsenic) being released in the production process and seeping into groundwater. The government is now offering financial support for exploratory drilling and opening up more land in national parks for surveys, which has produced plans for 14 new large-scale projects.
Most of the growth in Japan’s renewables had been in solar power, which began in 2012 when the government began requiring utilities to pay a higher price for solar power than they charge consumers for electricity. That helped not only the companies that generate solar power, but also made solar more attractive for consumers, who can sell unused electricity generated by their solar panels to their utility. However, when utilities complained about the costs of protecting the power grid from imbalances in supply and demand caused by the intermittency of solar power, the government lowered the price that utilities have to pay for its generation, hindering its growth. Bankruptcies in solar generating companies hit a record, totaling 31 in the first six months of the year, up 24 percent from the first half of last year. Further, the generating capacity of solar panels sold in Japan in the year through March was reduced by about 25 percent from the previous year.
Japan’s electricity demand is projected to remain flat through 2020 and deregulation of its power market has forced utilities to seek inexpensive fossil fuels (natural gas and coal) as they compete for customers in a tight market.
China
Coal accounts for the majority of China’s electricity production despite the fact that China installed a record 46.9 gigawatts of solar and wind capacity last year. As a result of these wind and solar units as well as some added nuclear capacity, the utilization rate of China’s coal plants declined from 50 percent to 46 percent during the past year. The boom in coal-plant building is underpinned by electricity prices, which have not fallen in line with the cost of building coal plants. According to the International Energy Agency (IEA), the cost of electricity in China is two-thirds higher than the average cost in Europe, but building a coal plant costs only half as much in China. Local Chinese authorities have sped up approvals for new coal plants and inexpensive financing is available. Further, coal mining and transport companies are diversifying into power plant construction to diversify their sources of income.
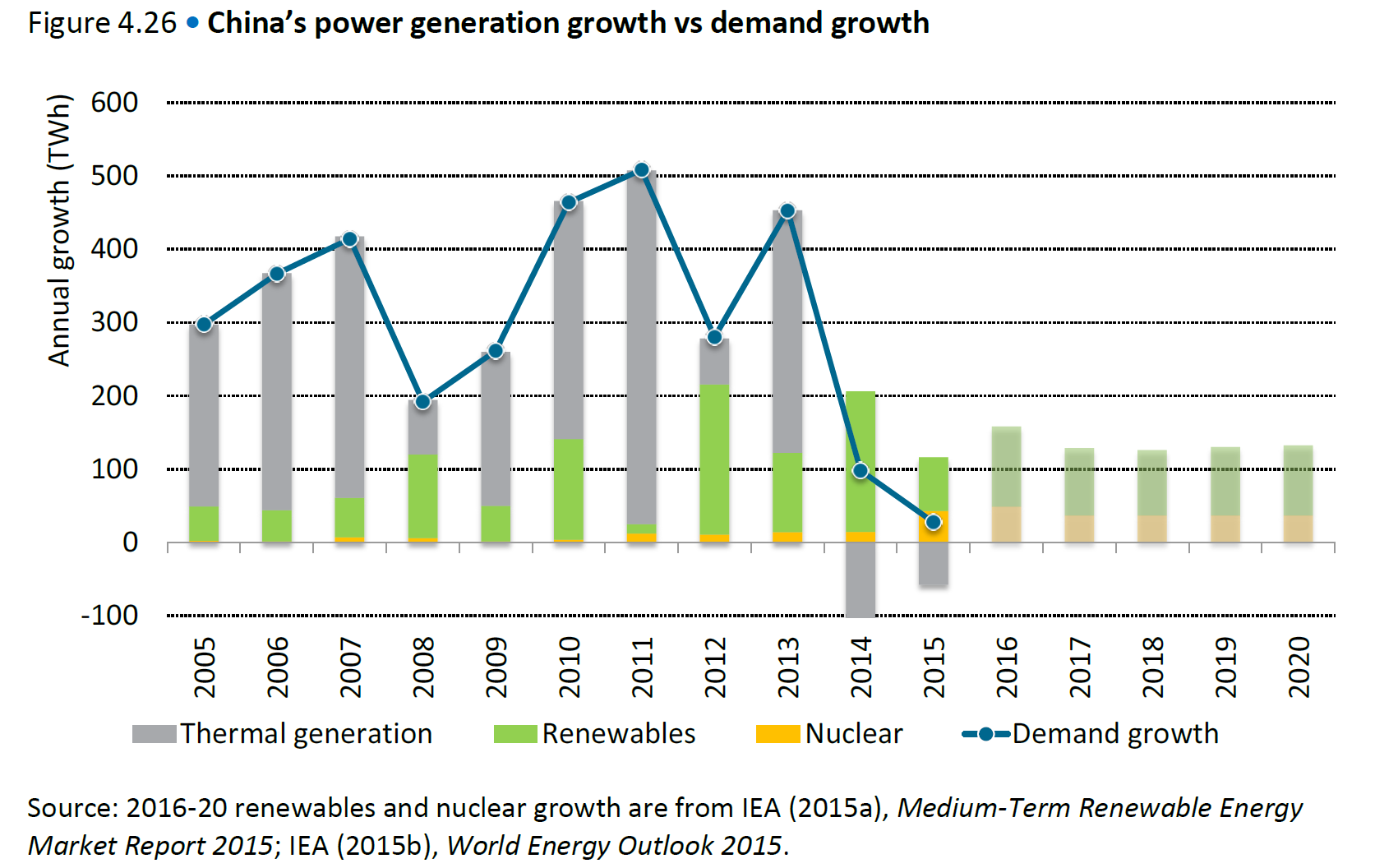
China’s electricity demand is also growing at a slower pace than it has historically. The IEA estimated that China’s electricity demand grew by just 2.7 percent in the first half of this year compared with the same period a year ago with about 21 gigawatts of new coal-fired plants coming online. The past two years of slowing demand growth has resulted in a narrowing of the electricity demand gap. According to IEA projections, renewable and nuclear energy are expected to be able to cover annual electricity demand growth of 2 to 2.5 percent through 2020, leaving little room for an expansion in coal-fired generation. (See graph below that shows IEA’s demand growth expectation for China and its expectations for increased generation to fill the gap.)
Conclusion
Needless to say, coal is still king in China despite projections that claim its growth in capacity is no longer needed and despite the government’s ratification of the Paris accord on climate change and its pledge to bring greenhouse-gas emissions to a peak no later than 2030. China is building coal-fired power plants because they are inexpensive to build despite lower electricity demand expectations by forecasters. Japan is also building coal-fired power plants, increasing the number of coal-fired power plants by almost 50 percent in the next 12 years. It is turning to low-cost coal and natural gas to replace its retired nuclear capacity despite the fact that it will need to import most of the fuel. Japan struggles with its goal to add higher cost renewable energy that requires government subsidies from taxpayers to survive.
[i] Bloomberg, China Seen Investing Too Much in Power Plants That Burn Coal, September 14, 2016, http://www.bloomberg.com/news/articles/2016-09-13/china-seen-investing-too-much-in-power-plants-that-burn-coal
[ii] Wall Street Journal, Japan’s Shift to Renewable Energy Loses Power, September 14, 2016, http://www.wsj.com/articles/japans-shift-to-renewable-energy-loses-power-1473818581