There is an obvious sense in which a dollar value can’t be placed on a human life. No decent parent, for example, would ever agree to losing a child’s life, for any amount of money. However, in practice we all make decisions that increase the risk of death, and in that sense, we trade off our own longevity for other goals.
In this context, economists can estimate the implied value of a human life, judged by the choices of the individuals themselves. One surprising implication of this approach is that costly government regulations not only reduce Americans’ standard of living, but they also indirectly lead to more deaths. In a modern economy, wealth is health, and so an inefficient regulation doesn’t merely reduce GDP—it also reduces average lifespans.
Explaining the “Value of a Statistical Life” (VSL)
Although very few people would kill themselves in exchange for a sum of money, in daily life we all engage in risky, life-threatening activities in order to save money. For example, putting aside psychological effects of worry, certain types of medical tests might give advance warning of having treatable conditions. Yet no woman would get, say, a monthly pap smear, because that would be a ridiculously costly strategy (including her time) in exchange for at best a miniscule increase in her expected lifespan.
Similarly, if consumers were willing to pay thousands of dollars more for safer vehicles, everyone could be driving around in tanks complete with extra padding, five-point harnesses, side air bags, and computer monitoring systems. But most Americans opt for cheaper vehicles in which they are more likely to die.
By analyzing consumer behavior, economists can come up with rough estimates of the implied “value of a statistical life” (VSL) that this behavior exhibits. To repeat, it’s not that someone flirts with certain death in exchange for $10 million.
Rather, it’s that a typical person might choose product X which costs $1 less than product Y, even though product X has a 4-in-ten-million chance of death compared to a 3-in-ten-million chance with product Y. In this hypothetical example, the person is willing to take on an extra 1-in-ten-million chance of dying, in order to save $1. This is the sense in which the person’s behavior implies a monetary value of a certain life (versus death) at $10 million.
How the EPA Explains Its Use of VSL
Our discussion above mirrors the EPA’s own explanation of how it uses VSL in cost/benefit analyses of federal regulations. Here’s is the EPA’s account:
The EPA does not place a dollar value on individual lives. Rather, when conducting a benefit-cost analysis of new environmental policies, the Agency uses estimates of how much people are willing to pay for small reductions in their risks of dying from adverse health conditions that may be caused by environmental pollution.
In the scientific literature, these estimates of willingness to pay for small reductions in mortality risks are often referred to as the “value of a statistical life.” This is because these values are typically reported in units that match the aggregate dollar amount that a large group of people would be willing to pay for a reduction in their individual risks of dying in a year, such that we would expect one fewer death among the group during that year on average. This is best explained by way of an example. Suppose each person in a sample of 100,000 people were asked how much he or she would be willing to pay for a reduction in their individual risk of dying of 1 in 100,000, or 0.001%, over the next year. Since this reduction in risk would mean that we would expect one fewer death among the sample of 100,000 people over the next year on average, this is sometimes described as “one statistical life saved.” Now suppose that the average response to this hypothetical question was $100. Then the total dollar amount that the group would be willing to pay to save one statistical life in a year would be $100 per person × 100,000 people, or $10 million. This is what is meant by the “value of a statistical life.” Importantly, this is not an estimate of how much money any single individual or group would be willing to pay to prevent the certain death of any particular person.
The EPA primer goes on to explain that the estimated VSL is used to rate the effectiveness of proposed federal regulations in cost/benefit terms. For example (this is my example, not theirs), suppose a very stringent rule on the emission of soot from smokestacks theoretically would reduce deaths by 2,000 lives, but at an aggregate cost to the economy of $80 billion in forfeited GDP. With these numbers, even on its own terms, such a regulation would save lives at a price of $40 million per life. This is much more than typical Americans spend with their own money to reduce risks and prolong their lifespans, and thus it indicates that the proposed regulation is inefficient because it implicitly forces Americans to “spend” much more on reducing a particular risk, rather than on other goods and services that they value more.
Now that I’ve explained it in my words, we can quote from the EPA primer to see that they feel the same way:
Agencies use estimates of values of risk reductions when conducting a benefit-cost analysis of a new policy or regulation that may affect public health. For example, many of the air and water pollution control regulations that are implemented by the EPA will reduce the risks of certain types of cancers, respiratory illnesses, and other diseases among large portions of the general public. Benefit-cost analysis compares the total willingness to pay for the health risk reductions from these policies to the additional costs that people will bear if the policies are adopted. These costs may come in the form of increased taxes, or, more commonly, increased prices of goods and services whose production, use, or disposal contributes to environmental pollution. The results of a benefit-cost analysis are presented to policy-makers and the public to help inform their judgments regarding whether or not a proposed policy should be adopted.
According to this particular EPA document, the default Value of a Statistical Life (VSL) for use in regulatory cost/benefit analysis is $7.4 million, measured in 2006 dollars. If we use the Consumer Price Index to relate 2006 to 2015 dollars, the current VSL for such analyses is about $8.8 million.
Thus, EPA’s own documentation admits that “saving lives” is not enough. In order to make sense, a proposed regulation must reduce deaths (in the aggregate) such that the implicit cost per life saved is no more than about $8.8 million. If it is higher than this, it means the regulation is inefficient, because it implicitly forces Americans to give up other potential uses of their income that they would have preferred to slight reductions in mortality rates.
In this world, there are always tradeoffs, and even if a proposed regulation genuinely saved lives (in the aggregate, statistical sense), it wouldn’t make sense to impose it if it also caused too much damage to the conventional economy.
Taking the Analysis Further: The Wealth-Health Connection
Thus far, some readers might not be too worked up about the possibility of an overbearing regulation. “Sure, a particular EPA rule could shrink the economy,” they might concede, “but if it saves lives, who cares if people cut back on how many pizzas they buy or movies they watch? Maybe the EPA should force them to ‘spend’ more on living longer.”
However, the deeper point with the wealth-health connection is that private individuals on their own devote some of their limited budgets to reducing mortality risks and thus prolonging their lifespans. Therefore, to the extent that a proposed regulation will make Americans poorer, then (in the aggregate) it could perversely cause an increase in fatalities. Indeed, even if a regulation is explicitly designed to reduce certain types of deaths, if it is very costly then it might, on net, kill more people than it saves.
The Scholarly Case
There is a voluminous academic literature seeking to quantify and explain the causal mechanisms behind the wealth-health connection. Hann, Lutter, and Viscusi wrote an excellent monograph for AEI / Brookings in 2000 that summarizes this work. When laying out the possible drawbacks to government regulation, their third effect is this:
Third, the costs of compliance with regulations pose risks. Compliance typically reduces the amount of private resources that people have to spend on a wide range of activities, including health care, children’s education, and automobile safety. When people have fewer resources, they spend less to reduce risks. The resulting increase in risk offsets the direct reduction in risk attributable to a government action. Moreover, if that direct risk reduction is small and the regulation is very ineffective relative to its cost, then total risk could rise instead of fall. [Hann, Lutter, and Viscusi p. 4, bold added.]
The authors then move on to analyze specific government regulations, using an estimate from “recent work by Lutter, Morrall, and Viscusi” that estimated “that an increase in income of about $15 million in a large U.S. population reduces mortality risk by one statistical death.”
Specifically, Lutter, Morrall, and Viscusi “construct a model in which people can reduce their risk of death through self-protective measures, but risk increases with increases in risky behaviors, such as smoking, overdrinking, and being overweight.” They find empirically that these risky behaviors tend to decrease as people’s income increases. This is how they generate the estimate that (at that time) an increase in income of $15 million (in 1990 dollars) in a U.S. community went hand in hand with one life saved in the aggregate.
Now for purists, I should note that it is not immediately obvious whether a reduction in income (through new government regulations, for example) would likewise cause an increase in (statistical) deaths. For example, suppose that people who are very disciplined and conservative (a) don’t smoke, drink, or overeat and (b) study hard in school and do a good job at work. In this case, we would also see a correlation between higher income and longevity, which wouldn’t necessarily cause more deaths if the government suddenly made everybody $1,000 poorer per capita.
However, the authors of the monograph do summarize the scholarly literature to show that there is indeed evidence of a specific causal mechanism linking higher income directly to risk reduction, through the purchase of healthier (but more expensive) food, getting better medical care, etc. Thus, our authors proceed with their claim that a policy that makes the community $15 million (in 1990 dollars) poorer will cause (on average) one extra death compared to the baseline.
A Specific Example
Hann, Lutter, and Viscusi then analyze what were (at that time) recent federal regulations, assessing them on the dimension of lives saved or forfeited. Below we reproduce just one example, to show how their analysis works. It pertains to a 1990 EPA rule described as “Land disposal restrictions for ‘third third’ scheduled wastes.”
TABLE: Hann et al. Analysis of Lives Lost From 1990 EPA Rule on Land Disposal Restrictions
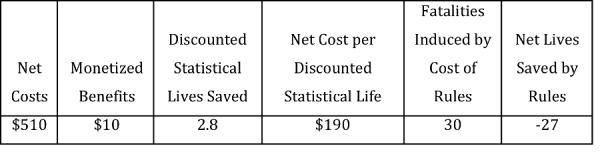
SOURCE: Table 3-1, Hann, Lutter, and Viscusi
In the table above, all dollar values are in millions (1995 dollars) annually.
The procedure works like this: The authors take the purported 2.8 statistical lives saved (per year) because of the regulation, and divide it into the estimated net cost of $510 million (per year). This works out to (roughly) $190 million per year per statistical life that the regulation saves due to its direct effect. Note that this is an order of magnitude higher than the standard estimates of the value of a statistical life.
Next, the authors take the net cost of the rule ($510 million) and divide by $17.3 million, which is the $15 million (from 1990) figure from the Lutter, Morrall, and Viscusi model updated to 1995 dollars. The answer is (roughly) 30 lives. This means that this particular EPA rule was so costly to the community that, by making Americans poorer, in the aggregate 30 people died each year who otherwise would have used the extra income in order to reduce risks and stay alive.
So, if the EPA rule directly saves 2.8 lives per year, but kills (by making Americans poorer) 30 lives per year, then on net the rule leads to 27 excess deaths per year. This is shown in the final column of the table. Note that negative “net lives saved” translates into positive net lives lost.
I should note that the monograph contains examples of regulations that the authors think do save lives on net. However, the big winners on this dimension are rules restricting minors from purchasing tobacco and Medicaid procedures. The more traditional idea of “federal regulations on business”—such as environmental quality standards coming from the EPA—in general do poorly, with many yielding net reductions in American lives.
Conclusion
Many people erroneously assume that federal regulations that purport to reduce mortality through their direct effects are obviously a good idea, because human life is more important than money. However, in reality, there is a well-established causal connection between wealth and health. Costly federal regulations make Americans poorer and thus indirectly lead to more deaths, because poorer people are less able to take advantage of private methods of prolonging their lives. If regulations are particularly inefficient, this indirect effect might overwhelm the direct benefit of the regulation, meaning that it not only makes Americans poorer, but actually kills them on net.